/Szkoła średnia/Zadania testowe/Funkcje/Różne

Zadanie nr 9789246

Która z poniższych funkcji nie ma ekstremów lokalnych?
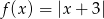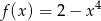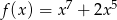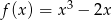
A) f(x ) = |x+ 3| B) f(x) = 2 − x 4 C) f(x ) = x7 + 2x5 D) f (x) = x3 − 2x

Wersja PDF

Rozwiązanie

Funkcja 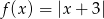f(x) = |x + 3| ma minimum lokalne (a nawet globalne) w x = − 3 .
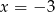Funkcja 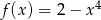f(x) = 2− x 4 ma maksimum lokalne (a nawet globalne) w x = 0 .
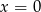Liczymy pochodne pozostałych dwóch funkcji

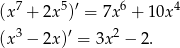
(x7 + 2x5)′ = 7x6 + 10x4 (x3 − 2x)′ = 3x2 − 2.

Pierwsza z powyższych funkcji ma nieujemną pochodną, więc funkcja ta jest rosnąca – w szczególności nie ma ekstremów lokalnych.

Pochodna drugiej funkcji ma dwa miejsca zerowe i zmienia w tych punktach znak, więc ma dwa ekstrema lokalne.

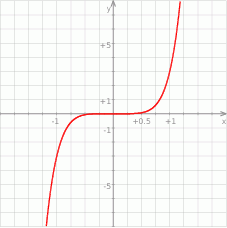
Na koniec dla ciekawskich wykres funkcji 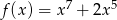f(x) = x 7 + 2x 5 .

PIC

 
Odpowiedź: C

Wersja PDF