Zadanie nr 2368306
Trójkąty 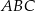 i
i 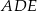 są równoboczne (zobacz rysunek). Punkty
są równoboczne (zobacz rysunek). Punkty 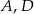 i
i 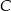 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 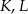 i
i 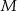 są środkami odcinków
są środkami odcinków 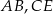 i
i 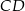 . Wykaż, że
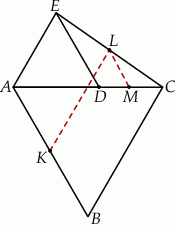
. Wykaż, że 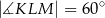 .
.
Rozwiązanie
Zauważmy, że proste 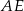 i
i 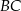 są równoległe (bo przecinają prostą
są równoległe (bo przecinają prostą 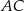 pod tym samym kątem). To oznacza, że czworokąt
pod tym samym kątem). To oznacza, że czworokąt 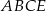 jest trapezem, a odcinek
jest trapezem, a odcinek 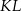 łączy środki jego ramion. Na mocy twierdzenia odwrotnego do twierdzenia Talesa (lub znanej własności trapezu) odcinek
łączy środki jego ramion. Na mocy twierdzenia odwrotnego do twierdzenia Talesa (lub znanej własności trapezu) odcinek 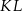 jest równoległy do podstaw tego trapezu, czyli
jest równoległy do podstaw tego trapezu, czyli 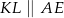 .
.
Odcinek 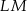 łączy środki boków trójkąta
łączy środki boków trójkąta 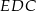 , więc jest równoległy do podstawy
, więc jest równoległy do podstawy 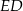 tego trójkąta.
tego trójkąta.
Uzasadniliśmy więc, że kąt między odcinkami 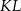 i
i 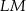 jest taki sam jak kąt między odcinkami
jest taki sam jak kąt między odcinkami 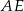 i
i 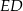 , czyli jest równy
, czyli jest równy 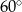 .
.

