Zadanie nr 2718204

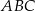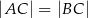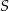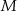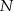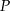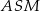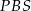W trójkąt równoramienny ABC ( |AC | = |BC | ) wpisano okrąg o środku . Punkty wspólne okręgu i trójkąta oznaczono literami , i . Uzasadnij, że trójkąty ASM i PBS są przystające.

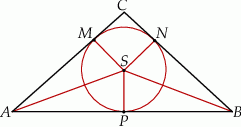
Rozwiązanie

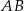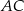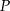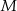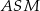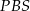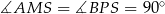Boki i są styczne do okręgu wpisanego w punktach i , więc trójkąty ASM i P BS są prostokątne: ∡AMS = ∡BP S = 90∘ .

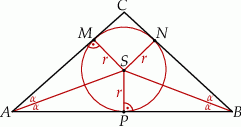
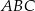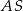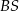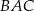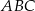Środkiem okręgu wpisanego w trójkąt ABC jest punkt wspólny dwusiecznych jego kątów, więc proste i są dwusiecznymi kątów BAC i ABC . Jeżeli więc oznaczymy 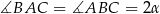∡BAC = ∡ABC = 2α (kąty te są równe, bo z założenia trójkąt 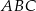ABC jest równoramienny), to

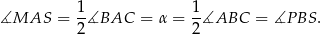
1 1 ∡MAS = --∡BAC = α = --∡ABC = ∡P BS . 2 2

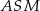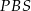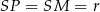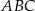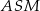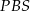To oznacza, że trójkąty ASM i PBS mają takie same kąty, czyli są podobne. Ponadto SP = SM = r , gdzie przez oznaczyliśmy promień okręgu wpisanego w trójkąt ABC . To oznacza, że trójkąty ASM i P BS są przystające.