Zadanie nr 5934841
W trójkącie prostokątnym 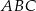 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 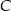 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 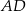 i
i 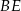 . Udowodnij, że
. Udowodnij, że 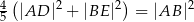 .
.
Rozwiązanie
Szkicujemy trójkąt prostokątny.
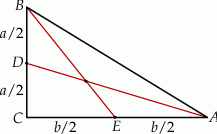
Jeżeli oznaczymy 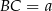 i
i 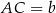 to z twierdzeń Pitagorasa w trójkątach
to z twierdzeń Pitagorasa w trójkątach 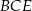 i
i 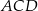 mamy
mamy
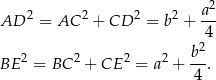
Dodajemy te równości stronami i mamy
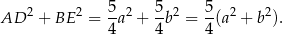
Na mocy twierdzenia Pitagorasa w trójkącie 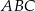 mamy więc
mamy więc