Zadanie nr 6839651
Środkowa 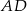 trójkąta
trójkąta 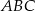 ma długość równą połowie długości boku
ma długość równą połowie długości boku 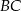 oraz
oraz 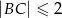 . Wykaż, że
. Wykaż, że 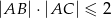 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
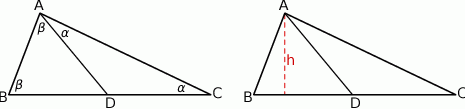
Zauważmy najpierw, że trójkąt 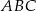 jest prostokątny. Rzeczywiście, trójkąty
jest prostokątny. Rzeczywiście, trójkąty 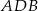 i
i 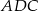 są równoramienne (bo
są równoramienne (bo 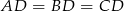 ), więc jeżeli oznaczymy ich kąty jak na rysunku powyżej, to
), więc jeżeli oznaczymy ich kąty jak na rysunku powyżej, to
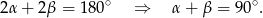
To z kolei oznacza, że 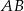 i
i 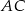 są przyprostokątnymi trójkąta prostokątnego
są przyprostokątnymi trójkąta prostokątnego 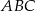 i
i