/Szkoła średnia/Funkcje/Trygonometryczna/Tożsamości

Zadanie nr 1241042

  • Sprawdź, czy równość
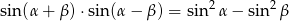
    sin (α+ β) ⋅sin (α− β) = sin2 α− sin 2β

    jest tożsamością trygonometryczną.

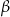  • Udowodnij, że jeżeli α i β są dwoma kątami trójkąta i 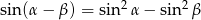sin (α− β) = sin2 α− sin 2β , to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
Wersja PDF

Rozwiązanie

  •  

    Sposób I

    Przekształcamy lewą stronę korzystając ze wzorów na sinus sumy i różnicy.

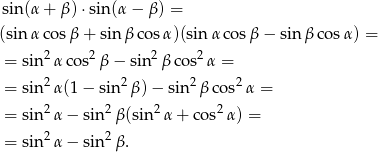
    sin(α + β) ⋅sin(α − β) = (sin α cosβ + sin βco sα)(sin αco sβ − sinβ cos α) = 2 2 2 2 = sin α cos β − sin βc os α = = sin 2α(1 − sin2 β)− sin 2β cos2α = = sin 2α − sin2β (sin 2α + cos2 α) = 2 2 = sin α − sin β .

    Jest to więc tożsamość trygonometryczna.

    Sposób II

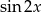    Przekształcamy prawą stronę korzystając ze wzoru na różnicę i sumę sinusów oraz ze wzoru na sin 2x .

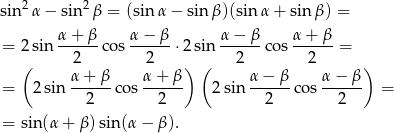
    sin 2α − sin2β = (sinα − sin β)(sinα + sin β) = α+ β α− β α − β α+ β = 2sin ------cos ------⋅2sin ------cos ------= ( 2 2 ) ( 2 2 ) = 2 sin α-+--βco s α-+-β 2sin α-−-β-cos α−--β- = 2 2 2 2 = sin (α+ β)sin(α − β ).

    Sposób III

    Podstawmy we wzorze na różnicę cosinusów

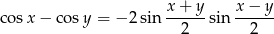
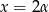    cosx − co sy = − 2 sin x-+-y-sin x-−-y- 2 2

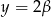    x = 2α i y = 2β . Mamy wtedy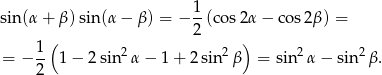

    1 sin (α+ β)sin(α − β ) = − --(cos2 α− cos2β ) = ( 2 ) = − 1- 1− 2sin2 α− 1+ 2sin2β = sin2 α− sin 2β. 2
  • Na mocy poprzedniego podpunktu równość 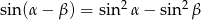2 2 sin(α − β) = sin α − sin β oznacza, że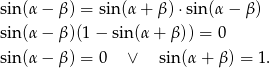
    sin(α − β ) = sin (α+ β) ⋅sin (α− β) sin(α − β )(1− sin(α + β)) = 0 sin(α − β ) = 0 ∨ sin(α + β) = 1.

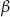    Ponieważ α i β są kątami trójkąta, pierwsza możliwość oznacza, że 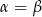α = β , czyli jest t o sytuacja trójkąta równoramiennego, a druga możliwość oznacza, że 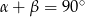∘ α + β = 9 0 , czyli trójkąt jest prostokątny.

Wersja PDF