Zadanie nr 2138082

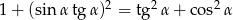Uzasadnij, że jeżeli jest kątem ostrym, to 2 2 2 1+ (sin α tg α) = tg α+ cos α .

Rozwiązanie

Przekształcamy daną równość w sposób równoważny.

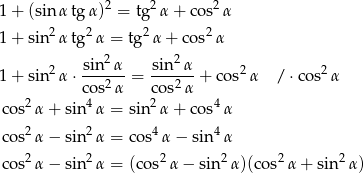
2 2 2 1 + (sin α tgα ) = tg α + cos α 1 + sin2α tg2α = tg 2α + cos2 α 2 2 1 + sin2α ⋅ sin-α = sin-α-+ cos2α / ⋅cos2α co s2α cos2α co s2α + sin4α = sin 2α + cos4 α co s2α − sin2α = cos4α − sin4 α 2 2 2 2 2 2 co s α − sin α = (cos α − sin α)(cos α + sin α)

Jedynka trygonometryczna oznacza, że wyrażenie w drugim nawiasie jest równe 1. To oznacza, że powyższa równość rzeczywiście jest spełniona.

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz