/Szkoła średnia/Funkcje/Trygonometryczna/Tożsamości

Zadanie nr 3676117

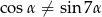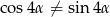Udowodnij, że jeżeli cos α ⁄= sin7 α i cos 4α ⁄= sin 4α to

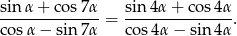
sin α + co s7α sin4α + co s4α --------------= ---------------. cosα − sin 7α cos 4α− sin 4α
Wersja PDF

Rozwiązanie

Sposób I

Przekształcamy daną równość.

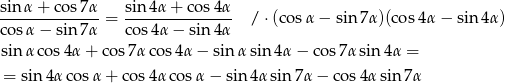
sin α + cos 7α sin 4α + cos 4α --------------= --------------- / ⋅(cosα − sin 7α)(cos 4α − sin4α ) cosα − sin 7α cos4α − sin 4α sin α cos4α + co s7α cos4 α− sin α sin 4α − co s7α sin 4α = = sin 4α cosα + co s4α cosα − sin 4αsin 7α − cos 4αsin 7α

Wyszło sporo składników, ale jak chwilę popatrzymy to powinno być widać, że mamy w tej równości cztery wzory na sinus/cosinus sumy/różnicy. Przekształćmy tę równość tak, aby było to wyraźniej widać.

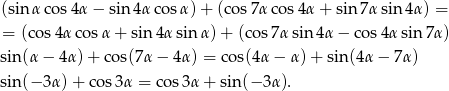
(sin αco s4α − sin 4αco sα) + (cos 7αco s4α + sin 7αsin 4α) = = (cos 4α cosα + sin 4αsin α)+ (cos7 αsin 4α− cos4α sin7 α) sin(α − 4 α)+ cos(7α − 4α) = cos(4α − α) + sin(4α − 7α ) sin(− 3α )+ co s3α = cos3α + sin(− 3α ).

Sposób II

Przekształcamy lewą stronę tak, aby pozamieniać sinus/cosinus 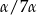α/7 α na sinus/cosinus 4α .

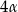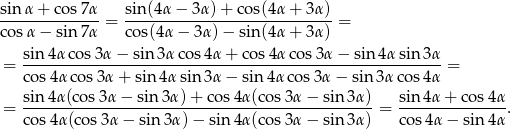
sin α+ cos7α sin(4α − 3 α)+ cos(4α + 3α) --------------= -----------------------------= cos α− sin 7α cos(4 α− 3α)− sin (4α + 3α) sin-4αco-s3α-−-sin-3αco-s4α-+-co-s4α-cos3α-−-sin-4α-sin-3α- = co s4α cos3 α+ sin 4α sin 3α − sin 4αco s3α − sin 3αco s4α = = sin-4α(cos-3α-−-sin3α-)+-co-s4α(co-s3α-−-sin-3α) = sin-4α-+-cos-4α. co s4α(co s3α − sin 3α)− sin 4α(co s3α − sin 3α) cos4α − sin 4α

Sposób III

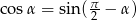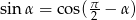Tym razem skorzystamy ze wzorów co sα = sin( π-− α) 2 i sin α = cos( π-− α) 2 oraz ze wzorów

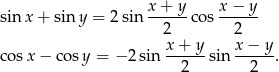
x-+-y- x-−-y- sinx + sin y = 2 sin 2 cos 2 x+ y x − y cos x− cosy = − 2sin ------sin ------. 2 2

Najpierw przekształcamy lewą stronę.

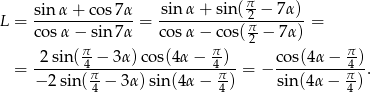
sin α+ cos7 α sin α + sin(π-− 7α) L = -------------- = -------------2π------ = co sα − sin7 α co sα − cos( 2-− 7α) 2 sin (π-− 3α )cos(4α − π) co s(4α− π-) = -------4π----------------4π-- = − ----------4π--. − 2 sin (4 − 3α )sin(4α − 4) sin (4α− 4)

Teraz przekształcamy prawą stronę

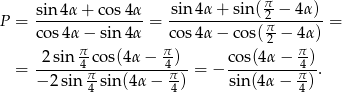
π- P = sin-4α-+-cos-4α = sin4α-+-sin(-2-−-4α)-= co s4α − sin 4α cos4α − c os(π2-− 4α ) 2 sin π-co s(4 α− π) cos(4α − π-) = -------4π----------4π- = − ---------π4-. − 2 sin-4 sin(4α − 4) sin (4α − 4-)

Zatem rzeczywiście 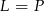L = P .

Wersja PDF