Zadanie nr 3778498
Udowodnij, że jeżeli 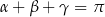 , to
, to
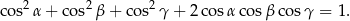
Rozwiązanie
Sposób I
Mamy udowodnić, że
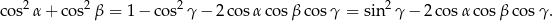
Wiemy, że 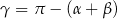 , więc
, więc
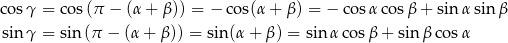
Mamy zatem
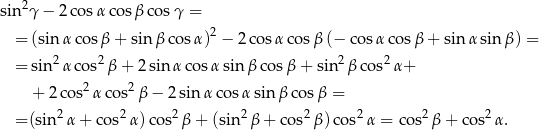
Sposób II
Tym razem skorzystamy ze wzorów
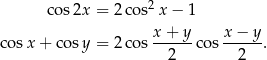
Mamy zatem
![2 2 2 1 2 cos α + co s β + cos γ = 2(1 + cos2 α+ 1+ cos2β )+ cos γ = = 1+ 1(co s2α + cos 2β) + cos2 γ = 1 + cos(α + β )cos(α − β )+ cos2γ = 2 = 1+ cos(π − γ )co s(α − β)+ cos2γ = 1− cosγ [cos(α − β )− co sγ] = = 1− cosγ [cos(α − β )− (co s(π − (α + β)))] = 1 − cos γ [co s(α− β)+ cos& (α−--β)-+-(α-+-β)- (α−--β)-−-(α-+-β)- = 1− cosγ ⋅2 cos 2 cos 2 = 1− 2cos αc osβ cosγ .](https://img.zadania.info/zad/3778498/HzadR5x.gif)
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że jeżeli 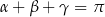 , to
, to
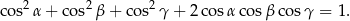
Sposób I
Mamy udowodnić, że
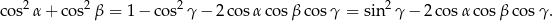
Wiemy, że 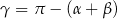 , więc
, więc
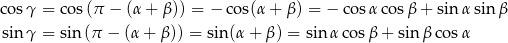
Mamy zatem
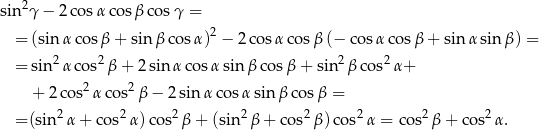
Sposób II
Tym razem skorzystamy ze wzorów
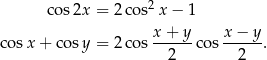
Mamy zatem
![2 2 2 1 2 cos α + co s β + cos γ = 2(1 + cos2 α+ 1+ cos2β )+ cos γ = = 1+ 1(co s2α + cos 2β) + cos2 γ = 1 + cos(α + β )cos(α − β )+ cos2γ = 2 = 1+ cos(π − γ )co s(α − β)+ cos2γ = 1− cosγ [cos(α − β )− co sγ] = = 1− cosγ [cos(α − β )− (co s(π − (α + β)))] = 1 − cos γ [co s(α− β)+ cos& (α−--β)-+-(α-+-β)- (α−--β)-−-(α-+-β)- = 1− cosγ ⋅2 cos 2 cos 2 = 1− 2cos αc osβ cosγ .](https://img.zadania.info/zad/3778498/HzadR5x.gif)
