/Szkoła średnia/Funkcje/Trygonometryczna/Tożsamości

Zadanie nr 6175911

Dodaj do ulubionych
Dodaj do rozwiązanych

Sprawdź, czy prawdziwa jest następująca tożsamość 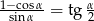1−cosα α sinα = tg 2 . Podaj konieczne założenia.

Rozwiązanie

Ze względu na 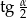α tg 2 mamy

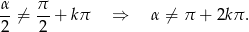
α- π- 2 ⁄= 2 + kπ ⇒ α ⁄= π + 2kπ.

Ze względu na 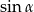sin α w mianowniku mamy 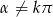α ⁄= kπ . Naturalnie ten warunek zawiera poprzedni. Przekształcamy lewą stronę.

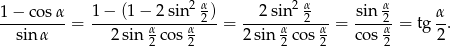
1 − cos α 1− (1− 2sin2 α) 2sin2 α sin α α --------- = --------α----α-2--= ------α--2-α = ----2α-= tg -. sin α 2 sin 2 cos 2 2 sin 2 cos 2 cos 2 2

 
Odpowiedź: Tożsamość jest prawdziwa dla α ⁄= kπ, k ∈ C

Wersja PDF