Zadanie nr 6663026

Wykaż, że

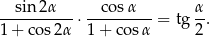
sin 2α cosα α ----------⋅ ---------= tg--. 1+ cos2α 1+ cosα 2

Wyznacz dziedzinę tej tożsamości.

Wersja PDF

Rozwiązanie

Korzystamy ze wzorów

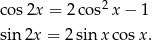
2 cos2x = 2co s x − 1 sin 2x = 2sin xcos x.

Przekształcamy lewą stronę tożsamości (zamieniamy konsekwentnie kąty tak, aby wszędzie mieć 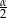α 2 ).

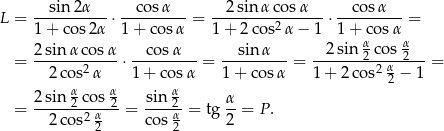
--sin-2α-- --cos-α-- --2sinα-cos-α--- --cosα--- L = 1 + cos 2α ⋅1 + cos α = 1+ 2cos2 α− 1 ⋅ 1+ cosα = α α = 2-sin-α-cosα-⋅ --cosα---= --sinα--- = --2-sin-2-cos-2-- = 2 cos2α 1+ cosα 1 + cos α 1 + 2 cos2 α2 − 1 2 sin α cos α sin α α = -----2---α-2 = ----2α-= tg-- = P . 2 cos2 2 co s2 2

Musimy jeszcze ustalić jaka jest dziedzina powyższej tożsamości. Muszą być spełnione 3 warunki:

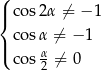
( |{ cos2α ⁄= − 1 cosα ⁄= − 1 |( α cos2 ⁄= 0

(ostatni warunek określa dziedzinę tangensa z prawej strony tożsamości). Szkicujemy cosinusa.

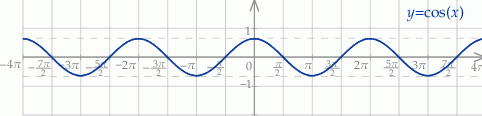
Z wykresu odczytujemy, że

( ( π |{ 2α ⁄= π + 2kπ |{ α ⁄= 2-+ kπ α ⁄= π + 2k π ⇐ ⇒ α ⁄= π + 2kπ |( α π- |( 2 ⁄= 2 + kπ α ⁄= π + 2kπ

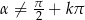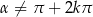Odpowiedź: α ⁄= π-+ kπ 2 i α ⁄= π + 2kπ , k ∈ Z