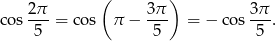Zadanie nr 8124954
Wykaż, że
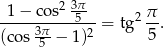
Rozwiązanie
Sposób I
Korzystamy ze wzorów
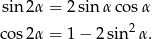
Przekształcamy lewą stronę tożsamości, którą mamy udowodnić
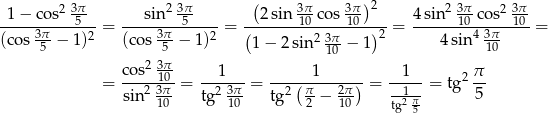
Sposób II
Przekształcamy tożsamość w sposób równoważny.
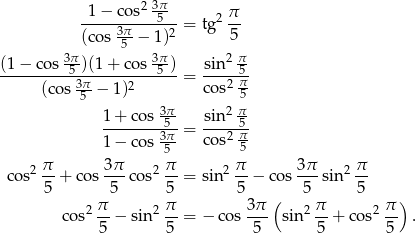
Korzystamy teraz z jedynki trygonometrycznej i wzoru
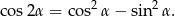
Mamy zatem
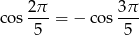
Ta równość jest oczywiście prawdziwa, bo