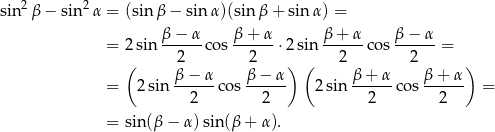Zadanie nr 8668505
Wykaż, że
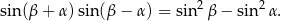
Rozwiązanie
Sposób I
Przekształcamy lewą stronę korzystając ze wzorów na sinus sumy/różnicy.
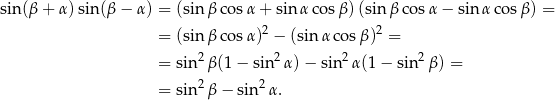
Sposób II
Przekształcamy prawą stronę korzystając ze wzorów na sumę/różnicę sinusów oraz ze wzoru na 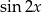 .
.
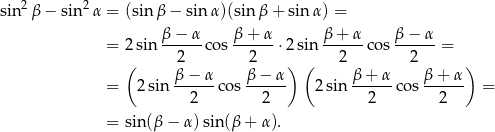
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że
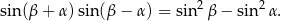
Sposób I
Przekształcamy lewą stronę korzystając ze wzorów na sinus sumy/różnicy.
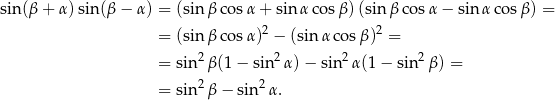
Sposób II
Przekształcamy prawą stronę korzystając ze wzorów na sumę/różnicę sinusów oraz ze wzoru na 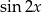 .
.