Zadanie nr 9532147
Uzasadnij, że dana równość 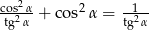 jest prawdziwa.
jest prawdziwa.
Rozwiązanie
Przekształcamy daną równość korzystając z definicji tangensa
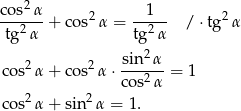
Otrzymana równość to jedynka trygonometryczna, która oczywiście jest prawdziwa.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że dana równość 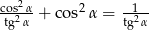 jest prawdziwa.
jest prawdziwa.
Przekształcamy daną równość korzystając z definicji tangensa
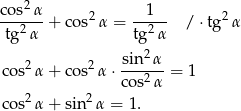
Otrzymana równość to jedynka trygonometryczna, która oczywiście jest prawdziwa.
