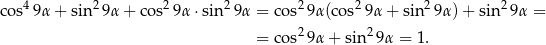Zadanie nr 2826936
Wykaż, że dla dowolnego kąta  ,
,
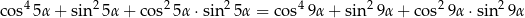
Rozwiązanie
Zauważmy, że
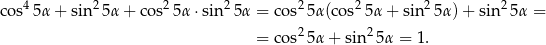
Dokładnie w ten sam sposób możemy obliczyć prawą stronę.
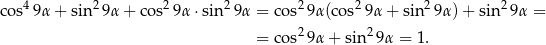
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnego kąta  ,
,
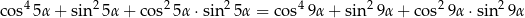
Zauważmy, że
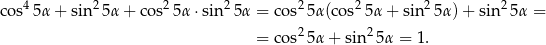
Dokładnie w ten sam sposób możemy obliczyć prawą stronę.