Bogactwo tożsamości trygonometrycznych jest niewątpliwie źródłem frustracji niejednego ucznia – trzeba dużo wprawy, żeby sprawnie się nimi posługiwać. Z drugiej strony, dzięki tym tożsamościom świat trygonometrii jest niezwykle ciekawy. Jedynka trygonometryczna Najpopularniejszą tożsamością trygonometryczną jest jedynka trygonometryczna
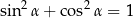
Jedynkę musi znać każdy i należy myśleć, że pozwala ona zamieniać 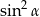 na
na 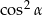 i odwrotnie.
i odwrotnie.
Zbadajmy zbiór wartości funkcji 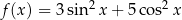 .
.
Z jedynki trygonometrycznej mamy
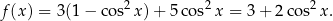
Korzystając teraz z nierówności 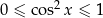 łatwo uzasadnić, że zbiór wartości
łatwo uzasadnić, że zbiór wartości 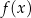 to przedział
to przedział 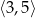 .
.
Wzory redukcyjne Jest wiele wzorów redukcyjnych i dokładnie omówiliśmy je w poradniku o wzorach redukcyjnych. Najważniejsze z nich to
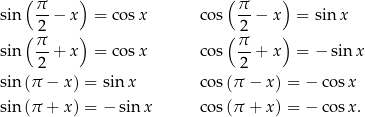
oraz
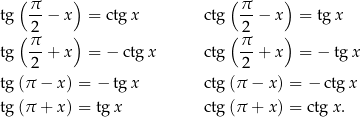
Wzory te pozwalają przesuwać argument funkcji trygonometrycznych o wielokrotność 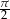 . Ponadto wzory z
. Ponadto wzory z 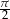 pozwalają zamieniać funkcję sinus/tangens na cosinus/cotangens i odwrotnie.
pozwalają zamieniać funkcję sinus/tangens na cosinus/cotangens i odwrotnie.
Obliczmy 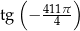 .
.
Liczymy
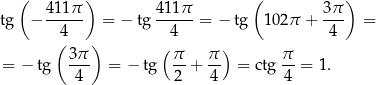
Rozwiążmy nierówność  .
.
Przekształcamy lewą stronę.
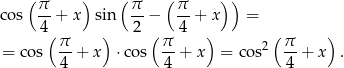
Mamy zatem
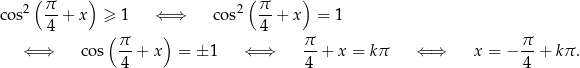
Podwojenie kąta Mamy dwa niezwykle użyteczne wzorki

Korzystając z jedynki trygonometrycznej, drugi z tych wzorów możemy zapisać w postaci
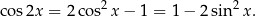
Wzory te bardzo często występują w zadaniach szkolnych, więc warto wyrobić sobie nawyk, że jak widzimy prawą stronę któregoś z tych wzorów, to dzwoni nam dzwoneczek 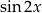 /
/ 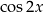 .
.
Wyznaczmy zbiór wartości funkcji 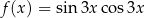 .
.
Ze wzoru na 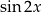 mamy
mamy
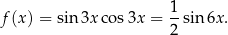
A więc zbiór wartości funkcji 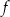 to przedział
to przedział 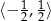 (bo zbiór wartości
(bo zbiór wartości 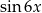 to przedział
to przedział 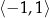 ).
).
Rozwiążmy równanie 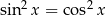 .
.
Ze wzoru na 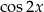 , możemy równanie przekształcić następująco
, możemy równanie przekształcić następująco
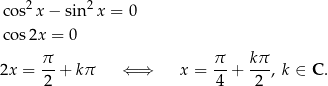
Sumy i różnice kątów Wzory trochę ogólniejsze od wzorów na sinus/cosinus podwojonego kąta:
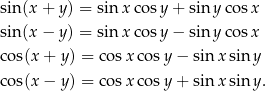
W zasadzie wystarczy pamiętać tylko pierwszy i trzeci z tych wzorów, dwa pozostałe dostajemy wstawiając do nich 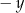 zamiast
zamiast 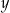 .
.
Oczywiste zastosowanie tych wzorów to możliwość obliczenia funkcji trygonometrycznych kąta 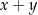 jeżeli znamy funkcje kątów
jeżeli znamy funkcje kątów  i
i 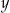 .
.
Obliczmy 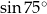 .
.
Liczymy
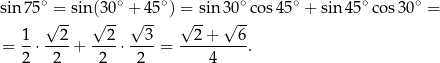
Uzasadnij, że jeżeli 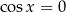 to
to 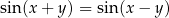 .
.
Na mocy powyższych wzorów mamy
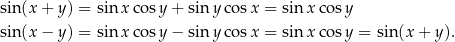
Sumy i różnice funkcji Ostatnia seria wzorków to wzory na sumy i różnice sinusów/cosinusów.
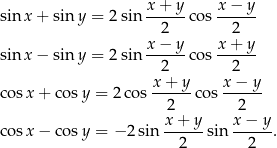
Wzory te są bardzo użyteczne w równaniach i nierównościach, gdyż pozwalają zamieniać równania typu suma równa 0, na równania typu iloczyn równy 0, a te drugie rozwiązuje się o wiele łatwiej.
Rozwiążmy równanie 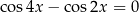 .
.
Z wzoru na różnicę cosinusów mamy
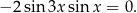
Czyli 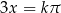 lub
lub 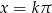 . Stąd
. Stąd 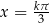 ,
, 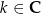 .
.

