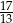/Szkoła średnia/Funkcje/Trygonometryczna/Wartość wyrażenia

Zadanie nr 5080706

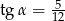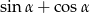Kąt α jest ostry oraz -5 tg α = 12 . Oblicz sin α+ cosα .

Wersja PDF

Rozwiązanie

Sposób I

Zacznijmy od obliczenia wartości 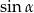sinα i cosα .

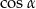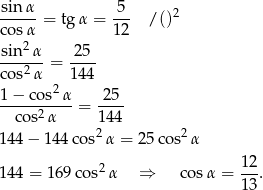
sin-α -5- 2 cos α = tg α = 1 2 / () 2 sin--α = 25-- cos2 α 144 1 − cos2 α 25 --cos2-α-- = 144- 2 2 144 − 144 cos α = 25 cos α 2 12 144 = 1 69co s α ⇒ cosα = --. 13

Opuszczając kwadrat korzystaliśmy z tego, że 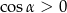cosα > 0 (bo α jest ostry). Obliczmy jeszcze sin α .

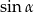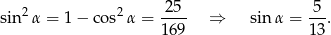
2 2 25 5 sin α = 1 − cos α = ---- ⇒ sin α = ---. 16 9 1 3

Teraz możemy obliczyć wartość podanego wyrażenia

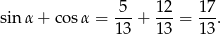
5-- 12- 17- sin α + co sα = 13 + 13 = 13 .

Sposób II

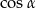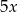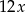Wartości funkcji trygonometrycznych sinα i cos α mogliśmy też obliczyć z trójkąta prostokątnego o przyprostokątnych 5x i 1 2x (żeby tangens był równy -5 12 ).

PIC

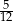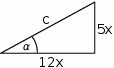
Z twierdzenia Pitagorasa mamy

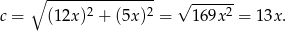
∘ --------------- √ ------ c = (12x)2 + (5x)2 = 169x2 = 1 3x.

Zatem

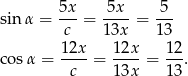
5x- -5x- 5-- sin α = c = 13x = 13 12x 12x 12 co sα = ----= ----= --. c 13x 13

Wartość wyrażenia 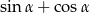sin α + cos α liczymy jak w poprzednim sposobie.  
Odpowiedź: 1173

Wersja PDF