/Szkoła średnia/Funkcje/Trygonometryczna/Wartość wyrażenia

Zadanie nr 5343126

Dodaj do ulubionych
Dodaj do rozwiązanych

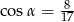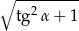Kąt α jest ostry 8 co sα = 17- . Oblicz ∘ --------- tg2 α+ 1 .

Rozwiązanie

Sposób I

Przekształcamy podane wyrażenie.

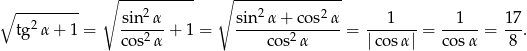
∘ --------- ∘ ----------- ∘ --------------- 2 sin-2α- sin2-α+--cos2α- ---1--- --1-- 17- tg α+ 1 = cos2α + 1 = co s2α = |cos α| = co sα = 8 .

Opuszczając wartość bezwzględną skorzystaliśmy z informacji o tym, że kąt α jest ostry.

Sposób II

Tym razem wyliczmy wartość 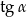tg α . Z jedynki trygonometrycznej mamy (bo α jest ostry)

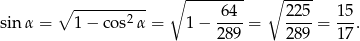
∘ -------- ∘ ---- ∘ ---------- 64 2 25 1 5 sin α = 1− co s2α = 1− ----= ---- = ---. 289 2 89 1 7

Zatem

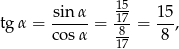
sinα 15- 15 tg α = ----- = -178-= ---, cosα 17- 8

oraz

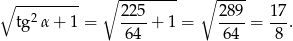
∘ --------- ∘ -------- ∘ ---- tg2 α+ 1 = 225-+ 1 = 289-= 17. 64 6 4 8

 
Odpowiedź: 178

Wersja PDF