Zadanie nr 5571404
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 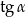 =3, oblicz wartość wyrażenia
=3, oblicz wartość wyrażenia 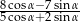 .
.
Rozwiązanie
Sposób I
Z założeń mamy
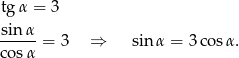
Obliczamy szukaną wartość
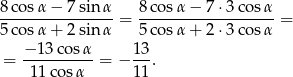
Sposób II
W danym wyrażeniu dzielimy licznik i mianownik przez 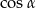 tak, aby otrzymać
tak, aby otrzymać 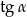 .
.
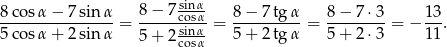
Odpowiedź: 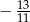
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 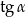 =3, oblicz wartość wyrażenia
=3, oblicz wartość wyrażenia 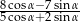 .
.
Sposób I
Z założeń mamy
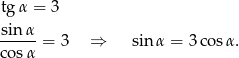
Obliczamy szukaną wartość
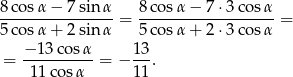
Sposób II
W danym wyrażeniu dzielimy licznik i mianownik przez 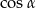 tak, aby otrzymać
tak, aby otrzymać 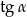 .
.
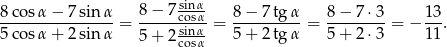
Odpowiedź: