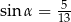Zadanie nr 6524568

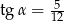Kąt jest ostry i 5- tg α = 12 . Oblicz sin α .

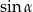Rozwiązanie

Sposób I

Liczymy

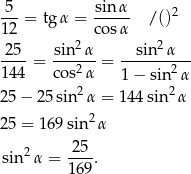
5 sin α ---= tg α = ----- / ()2 12 cosα -25- sin2α- --sin2-α-- 144 = cos2 α = 1 − sin2 α 2 2 25− 25sin α = 144 sin α 25 = 169 sin2α sin2α = -25-. 169

Ponieważ jest kątem ostrym, mamy stąd 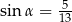sin α = 513- .

Sposób II

Kąt jest kątem w trójkącie prostokątnym o przyprostokątnych długości 5 i 12.

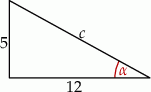
Korzystając z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej.

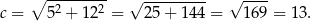
∘ --------- √ --------- √ ---- c = 52 + 122 = 25 + 1 44 = 169 = 13.

Zatem

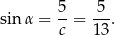
sinα = 5-= 5-. c 13

Odpowiedź: sin α = 513-

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz