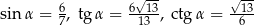/Szkoła średnia/Funkcje/Trygonometryczna/Wartość wyrażenia

Zadanie nr 7770293

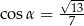Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego α jeżeli √-- cosα = -13- 7 .

Wersja PDF

Rozwiązanie

Sposób I

Najpierw liczymy 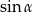sinα (z jedynki trygonometrycznej).

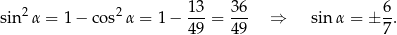
2 2 1-3 3-6 6- sin α = 1 − co s α = 1 − 4 9 = 4 9 ⇒ sin α = ± 7 .

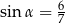Ponieważ α jest kątem ostrym, więc sinus jest dodatni, czyli sin α = 67 . Pozostałe funkcje wyznaczamy z definicji

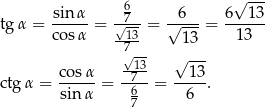
√ --- sinα 67 6 6 13 tgα = cos-α = -√13 = √----= -13--- -7-- 13 √13- √ --- ctgα = cos-α = --7- = --13. sinα 6 6 7

Sposób II

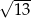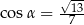Rysujemy trójkąt prostokątny o bokach √ --- 13 i 7 tak, aby √-- co sα = -173- .

PIC

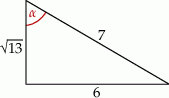
Na mocy twierdzenia Pitagorasa druga przyprostokątna ma długość

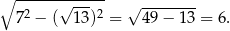
∘ ------√------ √ -------- 72 − ( 13 )2 = 49− 13 = 6.

Teraz łatwo odczytać pozostałe funkcje trygonometryczne kąta α .

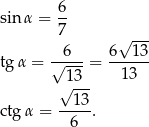
6- sin α = 7 √ --- tgα = √6---= 6--13- 13 1 3 √ 13- ctgα = ----. 6

 
Odpowiedź: 6√ 13- √ 13- sin α = 67 , tgα = -13-, ctgα = -6--

Wersja PDF