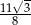Zadanie nr 9139008

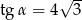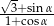Wiedząc, że jest kątem ostrym oraz √ -- tg α = 4 3 oblicz wartość wyrażenia √ - --3+sinα 1+cosα .

Rozwiązanie

Zacznijmy od obliczenia wartości 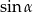sin α i cos α .

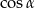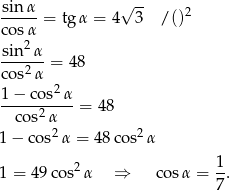
sin α √ -- ----- = tg α = 4 3 / ()2 co sα -sin-2α co s2α = 48 2 1-−-co-s-α = 48 co s2α 1 − cos2 α = 48 cos2α 1 = 4 9cos2 α ⇒ cosα = 1. 7

Opuszczając kwadrat korzystaliśmy z tego, że 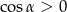cosα > 0 (bo jest ostry). Obliczmy jeszcze sin α .

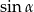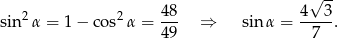
√ -- 2 2 48- 4--3- sin α = 1− cos α = 49 ⇒ sinα = 7 .

Teraz możemy obliczyć wartość podanego wyrażenia

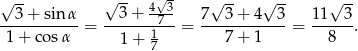
√ -- √ -- √- √ -- √ -- √ -- 3+ sin α 3+ 473- 7 3 + 4 3 11 3 -1+-co-sα--= ------1---= ---7-+-1----= --8---. 1 + 7

Odpowiedź: √ - 118-3

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz