Zadanie nr 6024649
Promień okręgu wpisanego w trójkąt równoboczny o boku  jest równy
jest równy 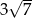 . Wynika stąd, że
. Wynika stąd, że
A) 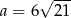 B)
B) 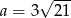 C)
C) 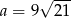 D)
D) 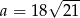
Rozwiązanie
Sposób I
Korzystamy z faktu, że promień okręgu wpisanego stanowi jedną trzecią wysokości trójkąta oraz
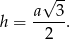
Zatem otrzymujemy
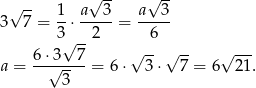
Sposób II
Robimy rysunek
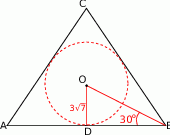
Liczymy tangens kąta 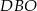
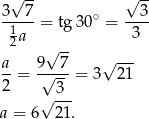
Odpowiedź: A

