/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt/Kwadrat

Zadanie nr 8824151

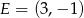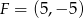Punkty E = (3,− 1) i F = (5 ,−5 ) są środkami dwóch sąsiednich boków kwadratu ABCD . Pole tego kwadratu jest równe
A) 10 B) 25 C) 40 D) 100

Wersja PDF

Rozwiązanie

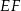Jeżeli narysujemy (lub przynajmniej wyobrazimy) sobie kwadrat ABCD to widać, że długość odcinka EF jest dwa razy mniejsza od długości przekątnej kwadratu (długość odcinka łączącego środki boków trójkąta ABC ).

PIC

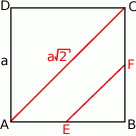
Zatem przekątna ma długość

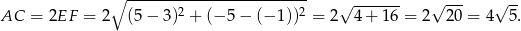
∘ ------------------------- √ ------- √ --- √ -- AC = 2EF = 2 (5− 3)2 + (− 5 − (− 1))2 = 2 4+ 16 = 2 20 = 4 5.

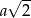Ponieważ przekątna kwadratu o boku a ma długość √ -- a 2 , w naszej sytuacji mamy

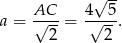
√ -- AC-- 4--5- a = √ --= √ --. 2 2

Pole jest więc równe

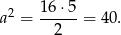
2 16 ⋅5 a = --2---= 4 0.

 
Odpowiedź: C

Wersja PDF