Zadanie nr 9731451
W trójkącie równoramiennym 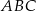 o podstawie
o podstawie 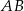 dane są:
dane są: 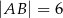 oraz
oraz 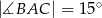 . Pole koła opisanego na tym trójkącie jest równe
. Pole koła opisanego na tym trójkącie jest równe
A) 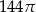 B)
B) 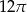 C)
C) 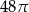 D)
D) 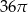
Rozwiązanie
Szkicujemy opisaną sytuację.
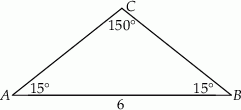
Trójkąt 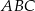 jest równoramienny, więc
jest równoramienny, więc
Jeżeli oznaczymy przez 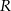 promień okręgu opisanego na trójkącie
promień okręgu opisanego na trójkącie 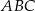 , to na mocy twierdzenia sinusów mamy
, to na mocy twierdzenia sinusów mamy
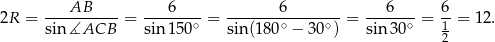
Zatem 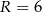 i pole koła opisanego na trójkącie
i pole koła opisanego na trójkącie 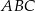 jest równe
jest równe
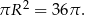
Odpowiedź: D

