/Szkoła średnia/Zadania testowe/Równania/Wielomianowe/Wyższego stopnia

Zadanie nr 5433046

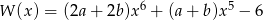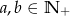Liczba -1 jest miejscem zerowym wielomianu 6 5 W (x) = (2a + 2b)x + (a + b)x − 6 i a ,b ∈ N + . Wynika stąd, że
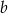A) a i b są liczbami o tej samej parzystości
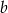B) a i b to liczby nieparzyste
C) jedna z liczb 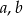a,b jest parzysta, a druga nieparzysta
D) 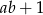ab + 1 jest liczbą parzystą

Wersja PDF

Rozwiązanie

Liczymy

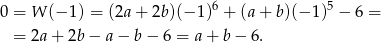
6 5 0 = W (− 1) = (2a+ 2b)(− 1) + (a+ b)(− 1) − 6 = = 2a + 2b − a − b − 6 = a + b − 6.

Zatem 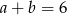a+ b = 6 .

Sposób I

Jeżeli suma dwóch liczb całkowitych jest liczbą parzystą, to obie muszą być parzyste lub obie muszą być nieparzyste.

Sposób II

Liczby naturalne spełniające równanie 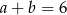a + b = 6 to

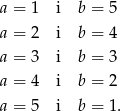
a = 1 i b = 5 a = 2 i b = 4 a = 3 i b = 3 a = 4 i b = 2 a = 5 i b = 1.

Widać, że obie liczby mają taką samą parzystość.  
Odpowiedź: A

Wersja PDF