Zadanie nr 8200757

Liczba pierwiastków całkowitych wielomianu 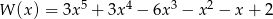5 4 3 2 W (x ) = 3x + 3x − 6x − x − x + 2 jest równa
A) 1 B) 2 C) 3 D) 4

Rozwiązanie

Pierwiastki całkowite danego wielomianu muszą być dzielnikami wyrazu wolnego, więc w rachubę wchodzą: 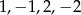1,− 1,2,− 2 . Sprawdzamy każdą z tych liczb

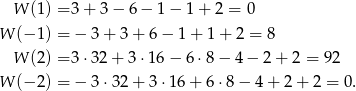
W (1) = 3 + 3 − 6 − 1 − 1 + 2 = 0 W (− 1) = − 3 + 3 + 6 − 1 + 1+ 2 = 8 W (2) = 3 ⋅32 + 3 ⋅16 − 6 ⋅8− 4− 2+ 2 = 92 W (− 2) = − 3 ⋅32 + 3 ⋅16+ 6⋅ 8− 4 + 2 + 2 = 0.

Wielomian ma więc 2 pierwiastki całkowite.
Odpowiedź: B

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz