/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 1885427

Dodaj do ulubionych
Dodaj do rozwiązanych

Określ liczbę pierwiastków równania 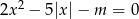2 2x − 5|x|− m = 0 w zależności od wartości parametru m .

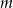Rozwiązanie

Jeżeli zapiszemy dane równanie w postaci

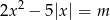
2 2x − 5|x | = m

to widać, że mamy wyznaczyć liczbę punktów wspólnych wykresu funkcji 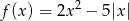f (x) = 2x2 − 5|x| z poziomą prostą 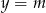y = m . Zauważmy, że

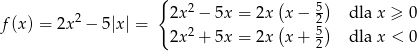
{ ( ) 2 2x2 − 5x = 2x x − 52 dla x ≥ 0 f (x) = 2x − 5|x| = 2x2 + 5x = 2x (x + 5 ) dla x < 0 2

Aby w miarę dokładnie naszkicować wykres funkcji 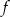f zauważmy, że wierzchołek paraboli z pierwszego wzoru ma współrzędne

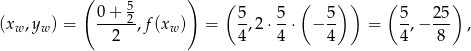
( ) ( ( ) ) ( ) 0-+-52- 5- 5- 5- 5- 25- (xw,yw ) = 2 ,f(xw) = 4 ,2⋅ 4 ⋅ − 4 = 4,− 8 ,

a współrzędne wierzchołka z drugiego wzoru to

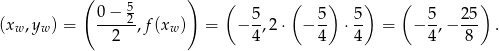
( ) ( ( ) ) ( ) 0 − 52 5 5 5 5 25 (xw,yw ) = ------,f(xw ) = − --,2⋅ − -- ⋅-- = − --,− --- . 2 4 4 4 4 8

Teraz pora na wykonanie wykresu.

PIC

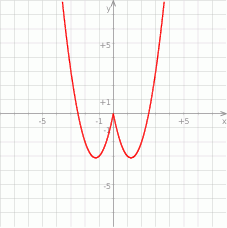
Z obrazka odczytujemy liczbę rozwiązań równania 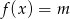f(x) = m .

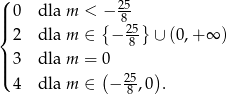
( 25 || 0 dla m < {− 8- } |{ 2 dla m ∈ − 25 ∪ (0,+ ∞ ) 8 ||| 3 dla m = (0 ) ( 4 dla m ∈ − 25-,0 . 8

 
Odpowiedź: ( 25 ||| 0 dla m < −{ 8 } { 2 dla m ∈ − 285 ∪ (0,+ ∞ ) | 3 dla m = 0 ||( ( ) 4 dla m ∈ − 285,0 .

Wersja PDF