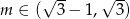Zadanie nr 2388426
Wyznacz wszystkie wartości parametru 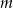 , dla których równanie
, dla których równanie 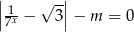 ma dwa pierwiastki, których iloczyn jest ujemny.
ma dwa pierwiastki, których iloczyn jest ujemny.
Rozwiązanie
Zapiszmy dane równanie w postaci
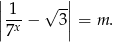
Naszkicujmy teraz wykres funkcji, którą mamy z lewej strony równania: rozpoczynamy od 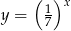 , potem przesuwamy ten wykres o
, potem przesuwamy ten wykres o 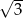 w dół i na koniec odbijamy część pod osią
w dół i na koniec odbijamy część pod osią 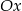 do góry.
do góry.
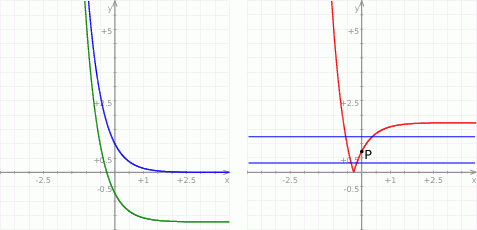
Z wykresu widać, że dane równanie ma dwa rozwiązania dla 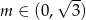 . Ponadto, jeżeli
. Ponadto, jeżeli 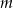 jest większe niż druga współrzędna punktu
jest większe niż druga współrzędna punktu 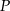 przecięcia narysowanego wykresu z osią
przecięcia narysowanego wykresu z osią 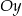 , to rozwiązania te będą miały różne znaki (bo będą po różnych stronach osi
, to rozwiązania te będą miały różne znaki (bo będą po różnych stronach osi 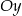 ). Drugą współrzędną punktu
). Drugą współrzędną punktu 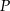 wyznaczmy podstawiając
wyznaczmy podstawiając 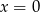 do wzoru funkcji.
do wzoru funkcji.
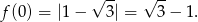
W takim razie równanie będzie miało dwa pierwiastki różnych znaków jeżeli 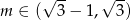 .
.
Odpowiedź: