/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 2443363

Dodaj do ulubionych
Dodaj do rozwiązanych

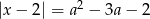Dla jakich wartości parametru a równanie 2 |x − 2| = a − 3a − 2 ma dwa pierwiastki różnych znaków?

Rozwiązanie

Sposób I

Na początek zastanówmy się kiedy (dla jakich 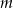m ) równanie 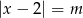|x − 2 | = m ma dwa pierwiastki różnych znaków. W tym celu rysujemy wykres funkcji 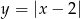y = |x − 2 | (jest to 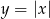y = |x | przesunięta o dwie jednostki w prawo) i patrzymy kiedy przecina on prostą 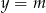y = m w dwóch punktach leżących po przeciwnych stronach osi Oy .

PIC

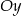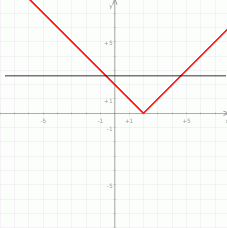
Z wykresu widać, że tak będzie dla 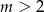m > 2 . Musimy zatem rozwiązać nierówność

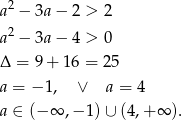
2 a − 3a − 2 > 2 a 2 − 3a − 4 > 0 Δ = 9 + 16 = 25 a = − 1, ∨ a = 4 a ∈ (− ∞ ,− 1) ∪ (4,+ ∞ ).

Sposób II

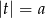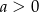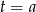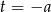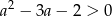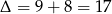Ogólnie równanie |t| = a ma dwa pierwiastki jeżeli a > 0 . W takim przypadku pierwiastki te są równe t = a i t = −a . Sprawdźmy więc na początek kiedy 2 a − 3a − 2 > 0 (czyli kiedy podane równanie ma dwa pierwiastki). Liczymy, Δ = 9 + 8 = 17 ,

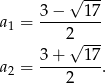
√ --- 3-−---17- a1 = 2 √ --- a2 = 3-+---17-. 2

A zatem

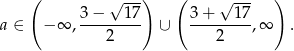
( √ --) ( √ --- ) a ∈ − ∞ , 3−---17- ∪ 3+----17,∞ . 2 2

Przy powyższym założeniu pierwiastkami równania są liczby 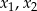x1,x2 takie, że

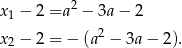
x 1 − 2 =a 2 − 3a − 2 2 x 2 − 2 = − (a − 3a− 2).

Przy naszym założeniu o dodatniości prawej strony równania, mamy 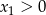x 1 > 0 . Pozostało sprawdzić kiedy x2 < 0 .

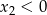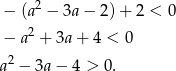
2 − (a − 3a− 2)+ 2 < 0 − a2 + 3a+ 4 < 0 a2 − 3a− 4 > 0.

Dalej, 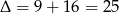Δ = 9 + 16 = 25

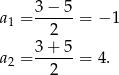
3−--5- a1 = 2 = − 1 3+ 5 a2 = ------= 4. 2

Zatem

a ∈ (− ∞ ,− 1) ∪ (4,∞ ).

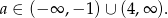
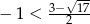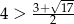W połączeniu z poprzednią nierównością (bo √-- 3−-17- − 1 < 2 i √ -- 3+--17 4 > 2 ) mamy

a ∈ (− ∞ ,−1 )∪ (4,∞ )

 
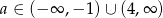
Odpowiedź: a ∈ (− ∞ ,− 1) ∪ (4,+ ∞ )

Wersja PDF