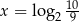/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 3506536

Wyznacz wszystkie wartości parametru 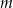m , dla których równanie 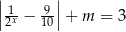| | || 1x − 9-||+ m = 3 2 10 ma dokładnie jedno rozwiązanie i rozwiązanie to jest liczbą dodatnią. Wyznacz to rozwiązanie.

Wersja PDF

Rozwiązanie

Zapiszmy dane równanie w postaci

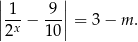
|| 1 9 || ||-x-− --|| = 3 − m . 2 10

Naszkicujmy teraz wykres funkcji, którą mamy z lewej strony równania: rozpoczynamy od 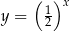( ) y = 1 x 2 , potem przesuwamy ten wykres o 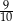-9 10 w dół i na koniec odbijamy część pod osią 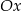Ox do góry.

PIC

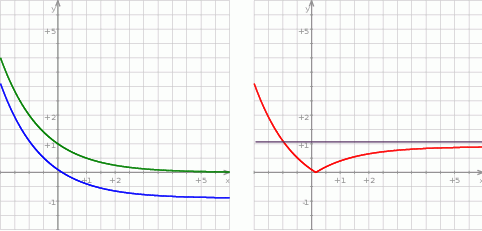
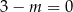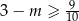Z wykresu widać, że dane równanie ma jedno rozwiązanie dla 3 − m = 0 lub 3 − m ≥ 190 . Jednak tylko w pierwszym przypadku rozwiązanie równania jest dodatnie. Zatem 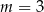m = 3 i mamy równanie

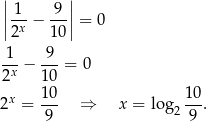
| | ||-1- 9-|| |2x − 10| = 0 1--− -9- = 0 2x 1 0 x 10- 10- 2 = 9 ⇒ x = log 2 9 .

 
Odpowiedź: 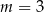m = 3 , 10 x = log2 9

Wersja PDF