/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 4487205

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj dla jakich wartości parametru 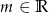m ∈ R równanie 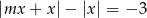|mx + x|− |x| = − 3 ma rozwiązanie.

Rozwiązanie

Ponieważ 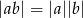|ab | = |a||b| , podane równanie możemy przekształcić następująco

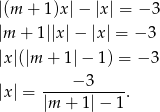
|(m + 1)x |− |x| = − 3 |m + 1||x|− |x | = − 3 |x|(|m + 1|− 1) = − 3 |x| = ----−-3----. |m + 1| − 1

Widać teraz, że równanie będzie miało rozwiązanie wtedy i tylko wtedy gdy 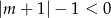|m + 1|− 1 < 0 (możemy wtedy wyliczyć x ).

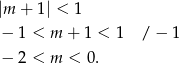
|m + 1| < 1 − 1 < m + 1 < 1 / − 1 − 2 < m < 0.

 
Odpowiedź: m ∈ (− 2,0)

Wersja PDF