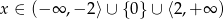/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 4814980

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 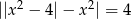2 2 ||x − 4| − x | = 4 .

Rozwiązanie

Sposób I

Jeżeli 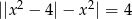2 2 ||x − 4 |− x | = 4 to

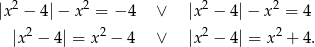
2 2 2 2 |x − 4|− x = − 4 ∨ |x − 4|− x = 4 |x2 − 4| = x2 − 4 ∨ |x2 − 4| = x2 + 4.

Zauważmy teraz, że lewe równanie będzie spełnione jeżeli tylko 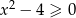x 2 − 4 ≥ 0 , czyli dla

x ∈ (−∞ ,− 2⟩ ∪ ⟨2,+ ∞ ).

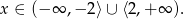
Zajmijmy się teraz prawym równaniem. Jeżeli 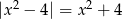2 2 |x − 4| = x + 4 to

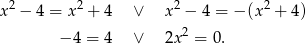
2 2 2 2 x − 4 = x + 4 ∨ x − 4 = − (x + 4) − 4 = 4 ∨ 2x2 = 0.

Otrzymujemy stąd dodatkowe rozwiązanie 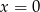x = 0 .

Sposób II

Zauważmy, że

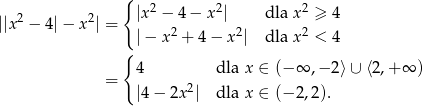
{ |x2 − 4 − x2| dla x2 ≥ 4 ||x2 − 4|− x2| = 2 2 2 | − x + 4 − x | dla x < 4 { = 4 dla x ∈ (− ∞ ,− 2⟩ ∪ ⟨2,+ ∞ ) |4 − 2x2| dla x ∈ (− 2,2 ).

Zatem 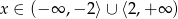x ∈ (− ∞ ,− 2⟩∪ ⟨2 ,+∞ ) lub

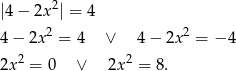
2 |4− 2x | = 4 4− 2x2 = 4 ∨ 4− 2x2 = − 4 2x2 = 0 ∨ 2x2 = 8.

Lewa równość daje 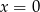x = 0 , a prawa jest sprzeczna z założeniem x ∈ (− 2,2) .

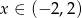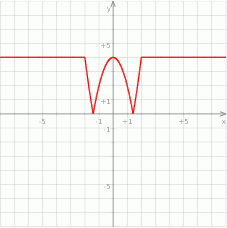
Na koniec dla ciekawskich wykres funkcji 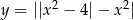y = ||x 2 − 4 |− x2| .

PIC

 
Odpowiedź: x ∈ (− ∞ ,− 2⟩ ∪ {0} ∪ ⟨2,+ ∞ )

Wersja PDF