Zadanie nr 5515560
Rozwiąż równanie 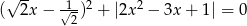 .
.
Rozwiązanie
Sposób I
Ponieważ oba składniki sumy są nieujemne, suma może być równa 0 tylko wtedy, gdy oba są 0. W szczególności
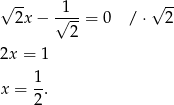
Łatwo sprawdzić, że dla 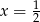 drugi składnik również jest równy 0.
drugi składnik również jest równy 0.
Sposób II
Przekształćmy podane równanie
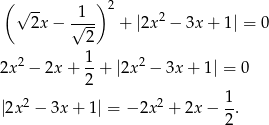
Aby zachodziło równanie postaci 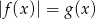 to musi być
to musi być 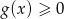 i
i 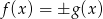 . Samo rozwiązanie równania
. Samo rozwiązanie równania 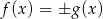 może dawać niepoprawne rozwiązania, bo np. -3=-3 ale
może dawać niepoprawne rozwiązania, bo np. -3=-3 ale 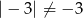 , ważne jest sprawdzenie czy prawa strona jest nieujemna. Zamiast sprawdzać nieujemność prawej strony (co w naszej sytuacji jest dość kłopotliwe), można sprawdzić poprawność otrzymanych rozwiązań. My postąpimy w ten drugi sposób.
, ważne jest sprawdzenie czy prawa strona jest nieujemna. Zamiast sprawdzać nieujemność prawej strony (co w naszej sytuacji jest dość kłopotliwe), można sprawdzić poprawność otrzymanych rozwiązań. My postąpimy w ten drugi sposób.
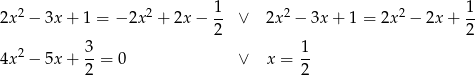
Liczymy, 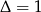 ,
, 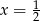 lub
lub 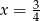 . Można sprawdzić, że tylko dla
. Można sprawdzić, że tylko dla 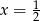 prawa strona jest nieujemna.
prawa strona jest nieujemna.
Dla ciekawskich wykresy prawej i lewej strony równania.
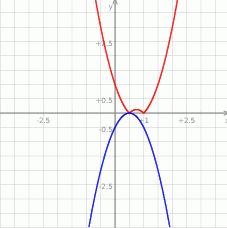
Odpowiedź: