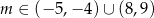/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 6134397

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 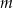m , dla których równanie

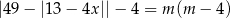
|49− |1 3− 4x ||− 4 = m (m − 4)

ma cztery różne rozwiązania, których iloczyn jest ujemny.

Rozwiązanie

Zapiszmy dane równanie w postaci

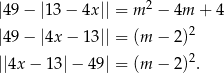
2 |49 − |13 − 4x|| = m − 4m + 4 |49 − |4x − 13|| = (m − 2)2 2 ||4x − 13|− 49| = (m − 2) .

(Skorzystaliśmy dwa razy z tego, że 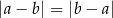|a− b| = |b − a| .) Szkicujemy teraz wykres lewej strony. Zaczynamy od wykresu funkcji 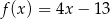f(x) = 4x − 13 , po czym odbijamy część znajdującą się poniżej osi 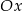Ox względem osi 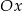Ox – otrzymujemy w ten sposób wykres funkcji 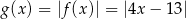g(x) = |f (x)| = |4x − 13| . Następnie ten wykres przesuwamy o 49 jednostek w dół i ponownie odbijamy do góry część wykresu znajdującą się poniżej osi Ox .

PIC

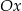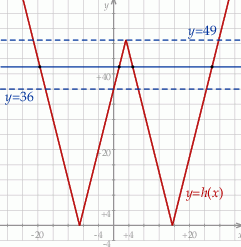
W wyniku tych operacji otrzymamy wykres

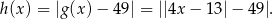
h(x ) = |g (x)− 49| = ||4x − 1 3|− 49 |.

Łatwo ponadto ustalić, że wykres ten przecina oś 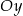Oy w punkcie o drugiej współrzędnej równej

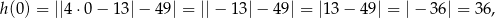
h(0) = ||4⋅0 − 1 3|− 49| = ||− 13|− 4 9| = |13 − 4 9| = |− 36| = 36 ,

a środkowe ostrze wykresu sięga do wysokości

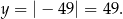
y = |− 4 9| = 49.

Z otrzymanego wykresu odczytujemy, że równanie 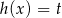h(x ) = t ma cztery różne rozwiązania dla

t ∈ (0,4 9).

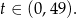
Ponadto, w przedziale 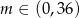m ∈ (0,36) dwa z tych rozwiązań są dodatnie, a dwa ujemne, dla 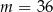m = 36 jedno z rozwiązań jest zerem, a dla 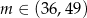m ∈ (36,49) trzy z rozwiązań są dodatnie, a jedno ujemne. W takim razie tylko w tym ostatnim przypadku iloczyn rozwiązań jest ujemny. Pozostało więc rozwiązać nierówność

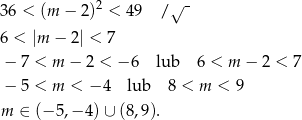
36 < (m − 2)2 < 49 / √ - 6 < |m − 2| < 7 − 7 < m − 2 < − 6 lub 6 < m − 2 < 7 − 5 < m < − 4 lub 8 < m < 9 m ∈ (− 5,− 4)∪ (8,9).

 
Odpowiedź: m ∈ (− 5,− 4)∪ (8,9)

Wersja PDF