/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 8643838

Dodaj do ulubionych
Dodaj do rozwiązanych

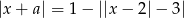Dla jakich wartości parametru a równanie |x + a| = 1 − ||x− 2|− 3 | ma dokładnie 2 rozwiązania?

Rozwiązanie

Szkicujemy wykresy obu stron równania. Lewa strona to wykres 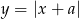y = |x + a| przesunięty poziomo tak, że jego wierzchołek znajduje się w punkcie 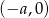(−a ,0 ) . A wykres prawej strony rysujemy zaczynając od wykresu 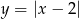y = |x − 2| . Potem przesuwamy ten wykres o 3 jednostki w dół i odbijamy część znajdującą się powyżej osi 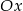Ox na dół (otrzymujemy w ten sposób wykres funkcji 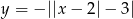y = − ||x − 2|− 3| ). Na koniec przesuwamy otrzymany wykres o 1 jednostkę do góry.

PIC

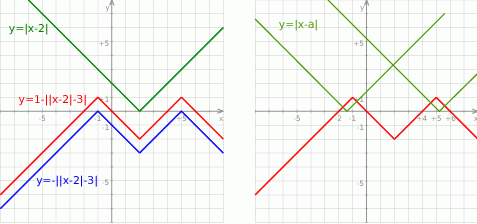
Z naszkicowanych wykresów widać, że dane równanie będzie miało dwa rozwiązania wtedy i tylko wtedy, gdy pierwsza współrzędna wierzchołka wykresu funkcji 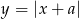y = |x + a| będzie w przedziale 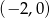(− 2,0) lub w przedziale 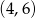(4,6) . Tak będzie gdy

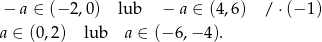
− a ∈ (− 2,0) lub − a ∈ (4 ,6) / ⋅(− 1) a ∈ (0,2) lub a ∈ (− 6,− 4).

 
Odpowiedź: a ∈ (− 6,− 4) ∪ (0,2)

Wersja PDF