Zadanie nr 9466613
Wyznacz liczbę rozwiązań równania 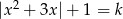 w zależności od parametru
w zależności od parametru 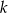 .
.
Rozwiązanie
Zadanie najprościej jest rozwiązać posługując się wykresem. Wykresem funkcji 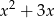 jest parabola o miejscach zerowych
jest parabola o miejscach zerowych 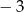 ,
, 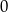 oraz wierzchołku w punkcie
oraz wierzchołku w punkcie 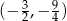 . Wykres funkcji
. Wykres funkcji 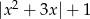 powstaje z wykresu
powstaje z wykresu 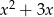 przez odbicie części poniżej osi
przez odbicie części poniżej osi 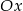 do góry, oraz przesunięcie całego wykresu o 1 jednostkę do góry.
do góry, oraz przesunięcie całego wykresu o 1 jednostkę do góry.
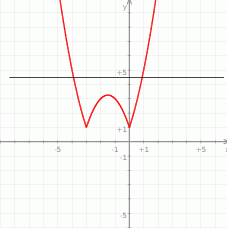
Widać teraz ile jest rozwiązań danego równania (czyli ile jest punktów wspólnych tego wykresu z prostą 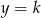 ).
).
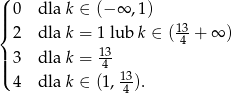
Odpowiedź: