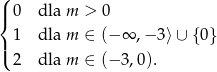Zadanie nr 9662624
Wyznacz w zależności od parametru 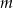 liczbę rozwiązań równania
liczbę rozwiązań równania 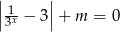 .
.
Rozwiązanie
Zapiszmy równanie w postaci
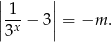
Sposób I
Szkicujemy wykres funkcji z lewej strony równania. Zaczynamy od 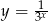 , potem przesuwamy tę funkcję o 3 jednostki w dół i mamy
, potem przesuwamy tę funkcję o 3 jednostki w dół i mamy 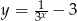 , a na koniec odbijamy część poniżej osi
, a na koniec odbijamy część poniżej osi 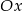 do góry.
do góry.
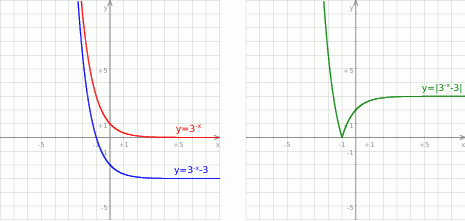
Gdy to zrobimy, to widać, że liczba rozwiązań powyższego równania jest równa
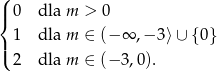
Sposób II
Jeżeli 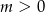 to prawa strona równania jest ujemna, czyli równanie jest sprzeczne.
to prawa strona równania jest ujemna, czyli równanie jest sprzeczne.
Jeżeli 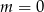 to mamy równanie
to mamy równanie
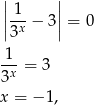
które ma jedno rozwiązanie.
Jeżeli 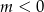 to mamy
to mamy
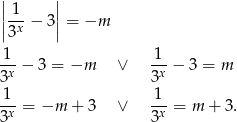
Jak wiemy zbiorem wartości funkcji wykładniczej jest przedział 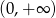 , więc lewe równanie ma zawsze rozwiązanie (bo
, więc lewe równanie ma zawsze rozwiązanie (bo 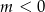 ), a prawe ma rozwiązanie tylko dla
), a prawe ma rozwiązanie tylko dla 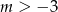 . Ponadto rozwiązania tych dwóch równań są różne, bo
. Ponadto rozwiązania tych dwóch równań są różne, bo 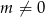 .
.
Podsumowując, liczba rozwiązań równania wyraża się wzorem.
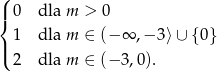
Odpowiedź: