/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 9860254

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 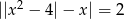2 ||x − 4| − x| = 2 .

Rozwiązanie

Jeżeli 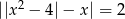2 ||x − 4|− x | = 2 to

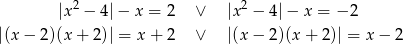
2 2 |x − 4|− x = 2 ∨ |x − 4| − x = − 2 |(x − 2)(x + 2)| = x + 2 ∨ |(x − 2)(x + 2 )| = x − 2

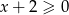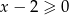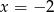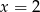Lewe równanie może być spełnione tylko, gdy x+ 2 ≥ 0 , a prawe dla x − 2 ≥ 0 . Ponadto widać, że liczby x = − 2 i x = 2 są rozwiązaniami równania, więc załóżmy dalej, że w lewym równaniu 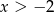x > − 2 , a w prawym x > 2 .

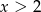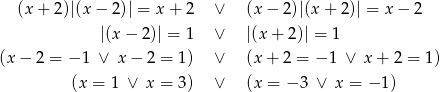
(x + 2)|(x − 2)| = x + 2 ∨ (x − 2)|(x + 2 )| = x − 2 |(x − 2)| = 1 ∨ |(x + 2)| = 1 (x − 2 = − 1 ∨ x − 2 = 1) ∨ (x + 2 = − 1 ∨ x+ 2 = 1) (x = 1 ∨ x = 3) ∨ (x = − 3 ∨ x = − 1)

Rozwiązania lewego równania spełniają warunek 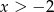x > − 2 , ale rozwiązania prawego nie spełniają warunku 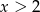x > 2 , więc musimy je odrzucić.

W sumie otrzymaliśmy więc cztery rozwiązania: 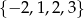{− 2,1,2,3} .

Na koniec, dla ciekawych, wykres prawej i lewej strony równania.

PIC

 
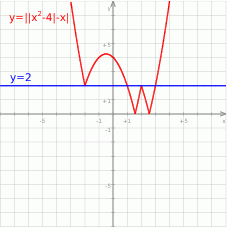
Odpowiedź: {− 2,1 ,2 ,3}

Wersja PDF