Zadanie nr 4401963
Czworokąt 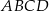 jest wpisany w okrąg, przy czym przekątna
jest wpisany w okrąg, przy czym przekątna 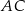 jest średnicą tego okręgu oraz
jest średnicą tego okręgu oraz 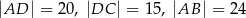 . Wtedy
. Wtedy
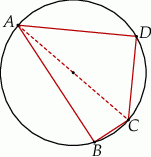
A) 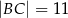 B)
B) 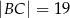 C)
C) 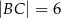 D)
D) 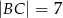
Rozwiązanie
Ponieważ odcinek 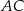 jest średnicą okręgu, trójkąty
jest średnicą okręgu, trójkąty 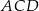 i
i 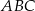 są prostokątne (kąt wpisany oparty na średnicy jest prosty).
są prostokątne (kąt wpisany oparty na średnicy jest prosty).
Liczymy korzystając z twierdzenia Pitagorasa.
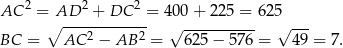
Odpowiedź: D

