Zadanie nr 5713756
Miary kątów pewnego czworokąta pozostają w stosunku 2:3:3:4. Wynika stąd, że najmniejszy kąt tego czworokąta ma miarę
A) 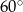 B)
B) 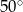 C)
C) 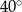 D)
D) 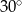
Rozwiązanie
Jeżeli oznaczymy miarę najmniejszego kąta czworokąta przez 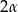 to pozostałe kąty mają miary
to pozostałe kąty mają miary 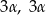 i
i 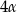 . Pozostało teraz skorzystać z tego, że suma kątów w czworokącie jest równa
. Pozostało teraz skorzystać z tego, że suma kątów w czworokącie jest równa 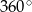 .
.
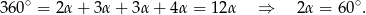
Odpowiedź: A

