Zadanie nr 6366093
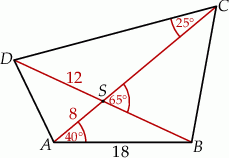
Odległości punktu 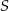 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 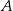 i
i 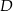 są równe
są równe 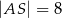 i
i 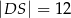 . Bok
. Bok 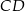 tego czworokąta ma długość
tego czworokąta ma długość
A) 27 B) 16 C) 24 D) 30
Rozwiązanie
Zauważmy, że
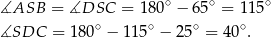
To oznacza, że trójkąty 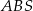 i
i 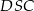 są podobne (mają dwa takie same kąty). Stąd
są podobne (mają dwa takie same kąty). Stąd
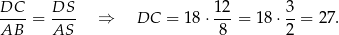
Odpowiedź: A

