Zadanie nr 5813784
Punkt 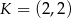 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 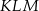 , w którym
, w którym 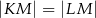 . Odcinek
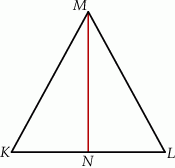
. Odcinek 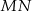 jest wysokością trójkąta i
jest wysokością trójkąta i 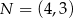 . Zatem
. Zatem
A) 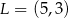 B)
B) 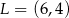 C)
C) 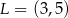 D)
D) 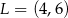
Rozwiązanie
Jeżeli narysujemy trójkąt równoramienny to widać,
że spodek wysokości 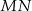 to dokładnie środek podstawy
to dokładnie środek podstawy 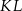 . Zatem
. Zatem
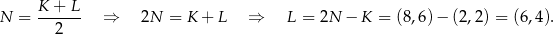
Odpowiedź: B

