Zadanie nr 7884340
Prosta 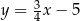 jest osią symetrii trójkąta
jest osią symetrii trójkąta 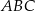 , w którym
, w którym 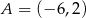 i
i 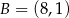 . Bok
. Bok 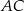 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu
A) 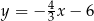 B)
B) 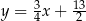 C)
C) 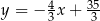 D)
D) 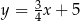
Rozwiązanie
Jeżeli trójkąt ma oś symetrii, to jest to trójkąt równoramienny.
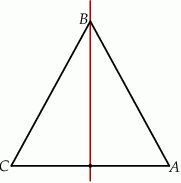
Ponadto, łatwo sprawdzić, że wierzchołek  należy do podanej prostej. W takim razie bok
należy do podanej prostej. W takim razie bok  jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego 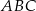 , więc jest prostopadły do podanej osi symetrii. W szczególności prosta
, więc jest prostopadły do podanej osi symetrii. W szczególności prosta 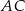 ma równanie postaci
ma równanie postaci 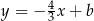 . Współczynnik
. Współczynnik 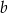 obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu  .
.
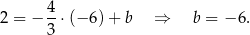
Odpowiedź: A

