/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt/Romb

Zadanie nr 1327548

Dodaj do ulubionych
Dodaj do rozwiązanych

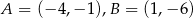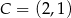Punkty A = (− 4,− 1),B = (1,− 6) i C = (2,1) są trzema kolejnymi wierzchołkami rombu 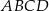ABCD . Pole tego rombu jest równe
A) 40 B) 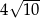√ --- 4 10 C) 80 D) 20

Rozwiązanie

Szkicujemy romb.

PIC

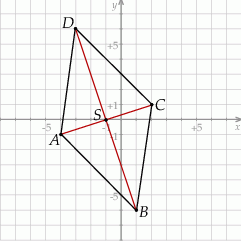
Przekątne rombu dzielą się na połowy, więc środek 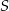S rombu ma współrzędne

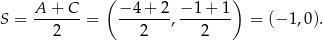
( ) S = A--+-C- = −-4-+-2, −-1-+-1 = (−1 ,0). 2 2 2

Sposób I

Romb składa się z 4 przystających trójkątów prostokątnych o przyprostokątnych

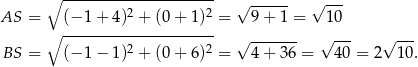
∘ --------------------- √ ------ √ --- AS = (− 1+ 4)2 + (0+ 1 )2 = 9+ 1 = 10 ∘ --------------------- √ ------- √ --- √ --- BS = (− 1− 1)2 + (0+ 6 )2 = 4+ 36 = 40 = 2 10.

Pole rombu jest więc równe

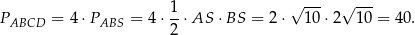
1 √ --- √ --- PABCD = 4 ⋅PABS = 4⋅ --⋅AS ⋅BS = 2 ⋅ 10 ⋅2 10 = 40. 2

Sposób II

Pole rombu możemy obliczyć ze wzoru na pole z przekątnymi. Obliczmy najpierw długości przekątnych.

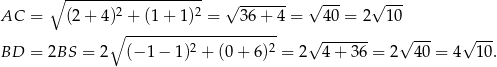
∘ ------------------- √ ------- √ --- √ --- AC = (2+ 4)2 + (1 + 1 )2 = 36+ 4 = 40 = 2 10 ∘ --------------------- √ ------- √ --- √ --- BD = 2BS = 2 (− 1− 1)2 + (0+ 6)2 = 2 4 + 36 = 2 40 = 4 10 .

Pole rombu jest więc równe

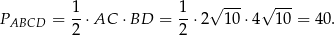
√ --- √ --- PABCD = 1-⋅AC ⋅BD = 1⋅ 2 10⋅ 4 10 = 40 . 2 2

 
Odpowiedź: A

Wersja PDF