/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 1519340

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że równanie 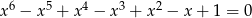6 5 4 3 2 x − x + x − x + x − x + 1 = 0 nie ma rozwiązań rzeczywistych.

Rozwiązanie

Sposób I

Jeżeli zapiszemy równanie w postaci

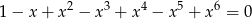
2 3 4 5 6 1− x+ x − x + x − x + x = 0

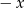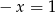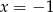to widać, że lewa strona równania jest sumą kolejnych wyrazów ciągu geometrycznego o ilorazie − x . Jeżeli − x = 1 to x = − 1 i widać, że liczba ta nie jest pierwiastkiem równania. Możemy zatem założyć, że 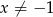x ⁄= − 1 i skorzystać ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego.

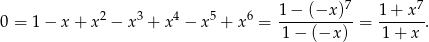
1− (−x )7 1 + x 7 0 = 1 − x + x2 − x3 + x4 − x5 + x6 = -----------= -------. 1 − (−x ) 1+ x

Otrzymane równanie jest sprzeczne, bo licznik zeruje się tylko dla 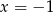x = − 1 , a liczba ta nie należy do dziedziny równania.

Sposób II

Zauważmy, że lewą stroną równania możemy zapisać w postaci

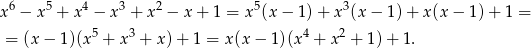
6 5 4 3 2 5 3 x − x + x − x + x − x+ 1 = x (x − 1) + x (x − 1 )+ x (x− 1)+ 1 = = (x− 1)(x5 + x3 + x) + 1 = x (x− 1)(x4 + x2 + 1)+ 1.

Wielomian stopnia 4 w nawiasie jest zawsze dodatni (jako suma kwadratów), więc powyższe wyrażenie będzie dodatnie, o ile tylko 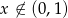x ⁄∈ (0,1) (bo wtedy x (x − 1) ≥ 0 ).

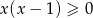Pozostało zająć się przypadkiem 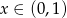x ∈ (0,1 ) . Teraz lewą stronę równania zapiszmy następująco:

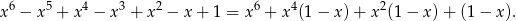
6 5 4 3 2 6 4 2 x − x + x − x + x − x+ 1 = x + x (1 − x )+ x (1− x )+ (1 − x ).

Jest jasne, że dla 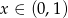x ∈ (0,1) wyrażenie to jest dodatnie.

Wersja PDF