/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 1685142

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 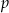p , dla których równanie 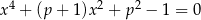4 2 2 x + (p + 1)x + p − 1 = 0 ma dokładnie dwa różne pierwiastki.

Rozwiązanie

Podstawiamy 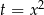2 t = x i mamy równanie kwadratowe

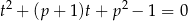
2 2 t + (p+ 1)t+ p − 1 = 0

Aby wyjściowe równanie miało dokładnie dwa pierwiastki, powyższe równanie kwadratowe musi mieć dokładnie jeden pierwiastek dodatni (da on nam dwa x -y). Sprawdźmy kiedy równanie ma pierwiastki.

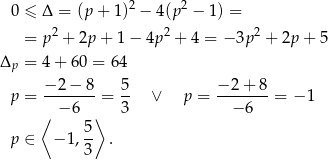
0 ≤ Δ = (p + 1)2 − 4(p2 − 1) = 2 2 2 = p + 2p + 1− 4p + 4 = − 3p + 2p + 5 Δp = 4 + 60 = 64 p = −-2-−-8 = 5- ∨ p = −-2-+-8 = − 1 ⟨ − 6 ⟩ 3 − 6 5 p ∈ − 1,3- .

Sprawdźmy teraz kiedy dokładnie jeden z pierwiastków jest dodatni.

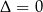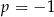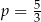Na początek sprawdźmy sytuacje gdy Δ = 0 , czyli p = − 1 lub 5 p = 3 . Mamy wtedy równania

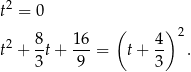
2 t = 0 ( ) 2 t2 + 8t+ 16-= t + 4- . 3 9 3

Widać, że w obu przypadkach jest źle.

Jeżeli 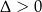Δ > 0 to pytamy się kiedy pierwiastki są różnych znaków (żeby dostać 2, a nie 4 wartości x ). Na mocy wzorów Viète’a tak będzie, gdy

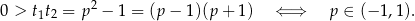
2 0 > t1t2 = p − 1 = (p − 1)(p + 1) ⇐ ⇒ p ∈ (− 1,1).

W połączeniu z warunkiem na 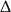Δ -ę daje to nam p ∈ (− 1,1) .  
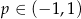Odpowiedź: p ∈ (− 1,1 )

Wersja PDF