/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 3247088

Dodaj do ulubionych
Dodaj do rozwiązanych

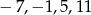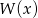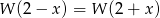Liczby − 7 ,− 1 ,5 ,11 są miejscami zerowymi wielomianu czwartego stopnia W (x) . Wykaż, że dla dowolnej liczby rzeczywistej x spełniona jest równość W (2− x ) = W (2 + x) .

Rozwiązanie

Podane miejsca zerowe wielomianu 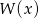W (x ) oznaczają, że

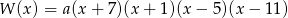
W (x ) = a(x + 7)(x + 1)(x − 5)(x − 1 1)

dla pewnej liczby a . Mamy zatem

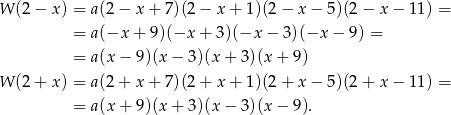
W (2 − x ) = a(2− x+ 7)(2− x + 1)(2 − x − 5)(2 − x − 11) = = a(−x + 9)(−x + 3)(−x − 3)(−x − 9) = = a(x− 9)(x − 3)(x + 3)(x + 9) W (2 + x ) = a(2+ x+ 7)(2+ x + 1)(2 + x − 5)(2 + x − 11) = = a(x+ 9)(x + 3)(x − 3)(x − 9).

Zatem rzeczywiście 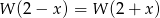W (2− x) = W (2 + x ) .

Wersja PDF