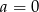/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 3745322

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 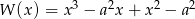3 2 2 2 W (x) = x − a x + x − a , gdzie |a| ⁄= 1 .

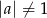  • Oblicz sumę pierwiastków tego wielomianu.
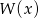  • Wyznacz wartość parametru a , dla której suma kwadratów pierwiastków wielomianu W (x) jest możliwie najmniejsza.

Rozwiązanie

  • Rozkładamy wielomian na czynniki
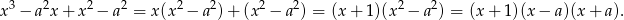
    x 3− a2x + x2 − a2 = x(x 2− a2)+ (x2− a2) = (x+ 1)(x 2− a2) = (x + 1)(x − a)(x + a).

    Zatem pierwiastki wielomianu to 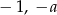− 1 , −a oraz a . Suma pierwiastków jest więc równa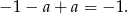

    − 1− a+ a = − 1.

     
    Odpowiedź: -1

  • Z poprzedniego podpunktu wiemy, że suma kwadratów pierwiastków wielomianu 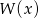W (x) jest równa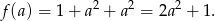
    f(a) = 1 + a 2 + a2 = 2a 2 + 1 .

    Wykresem tej funkcji jest parabola o ramionach skierowanych w górę, zatem najmniejszą wartość otrzymamy w wierzchołku, czyli dla a = 0 .  
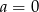    Odpowiedź: a = 0

Wersja PDF