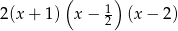/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 3869762

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 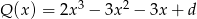3 2 Q(x ) = 2x − 3x − 3x + d .

  • Liczba 1 jest pierwiastkiem tego wielomianu. Oblicz d .
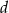  • Dla 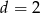d = 2 przedstaw wielomian 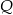Q w postaci iloczynu wielomianów stopnia pierwszego.

Rozwiązanie

  • Ponieważ 1 jest pierwiastkiem, to
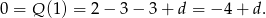
    0 = Q (1) = 2− 3− 3+ d = − 4 + d.

    Stąd d = 4 .  
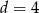    Odpowiedź: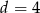 d = 4

  • Żeby znaleźć pierwiastki całkowite (lepiej zacząć od nich zanim spróbujemy z wymiernymi), wstawiamy do wielomianu dzielniki wyrazu wolnego, czyli liczby -1,1,-2,2 tak długo aż dla jakiejś wyjdzie 0 – wychodzi już dla -1 . Jak już mamy pierwiastek, to dzielimy wielomian przez 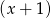(x + 1 ) . Robimy to tak jak umiemy, schemat Hornera, dzielenie wielomianów lub grupowanie odpowiednich czynników. My zrobimy to tą ostatnią metodą: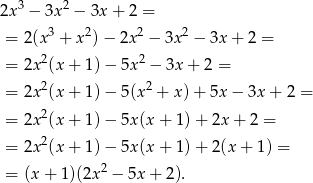
    3 2 2x − 3x − 3x + 2 = = 2 (x 3 + x 2)− 2x 2 − 3x2 − 3x + 2 = 2 2 = 2x (x+ 1)− 5x − 3x + 2 = = 2x 2(x+ 1)− 5(x2 + x)+ 5x − 3x + 2 = = 2x 2(x+ 1)− 5x(x + 1) + 2x + 2 = 2 = 2x (x+ 1)− 5x(x + 1) + 2(x + 1) = = (x + 1 )(2x2 − 5x + 2).

    Pozostało teraz rozłożyć 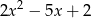2 2x − 5x+ 2 . Robimy to standardowo, 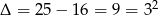Δ = 25− 16 = 9 = 3 2 . Stąd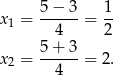

    5 − 3 1 x1 = ------= -- 4 2 5-+-3- x2 = 4 = 2.

    Mamy zatem szukany rozkład

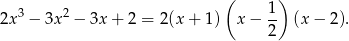
    ( ) 2x3 − 3x2 − 3x + 2 = 2(x+ 1) x − 1- (x− 2). 2

     
    Odpowiedź: ( ) 2(x + 1) x − 1 (x − 2) 2

Wersja PDF